Technical note: Problem-specific variators in a genetic algorithm for the optimization of drinking water networks

Genetic algorithms can be a powerful tool for the automated design of optimal drinking water distribution networks. Fast convergence of such algorithms is a crucial factor for successful practical implementation at the drinking water utility level. In this technical note, we therefore investigate the performance of a suite of genetic variators that was tailored to the optimization of a least-cost network design. Different combinations of the variators are tested in terms of convergence rate and the robustness of the results during optimization of the real-world drinking water distribution network of Sittard, the Netherlands. The variator configurations that reproducibly reach the furthest convergence after 10⁵ function evaluations are reported. In the future these may aid in dealing with the computational challenges of optimizing real-world networks.

1 Introduction

Optimization techniques have been applied to the design (or more specifically, the dimensioning) of water networks for decades (see Bieupoude et al., 2012, and De Corte and Sörensen, 2013, for overviews). A widely applied approach is that of genetic algorithms (GAs) (Holland, 1975; Goldberg, 1989) and other members of the overarching family of evolutionary algorithms (EAs) (Maier et al., 2014). Though the classic genetic algorithm is very powerful, the various mechanisms of the genetic algorithm are commonly expanded, replaced or combined with heuristic tricks or complete heuristic algorithms to improve performance (as reviewed by e.g. El-Mihoub et al., 2006). The algorithms which include these are commonly referred to as hybrid genetic algorithms (HGAs) or memetic algorithms (MAs). An overview of these approaches is summarized below. Following one of the approaches, a selection of custom heuristic variators has been implemented in Gondwana, a generic optimization tool for drinking water networks (van Thienen and Vertommen, 2015). In this paper, these variators are described and it is demonstrated how they contribute to significantly faster convergence in an optimization problem case study.

2 Hybrid genetic algorithms

A cornerstone of the HGA approach (Krasnogor and Smith, 2005; El-Mihoub et al., 2006) is the observation that classic GAs are especially well suited for quickly locating global optima in the solution space but subsequently have difficulty converging to the optimum locally within a reasonable number of iterations. To mitigate this, GAs are augmented with local search (LS) methods. These are algorithms that iteratively modify a given solution towards a predefined optimization criterion. LS methods find local optima relatively quickly but are generally unable to escape this local optimum in favour of a possibly different global optimum. The resulting HGA therefore profits from the strengths of both techniques and yields better solutions. El-Mihoub et al. (2006) identify the following general ways in which GA capabilities can be expanded through hybridization:

1. A GA solution can be improved by running it through a LS method. This can be done to improve the final solution of the GA. Alternatively, the LS algorithm can be applied to refine intermediate solutions to promote the representation of different promising areas of the solution space within the population.

2. The number of iterations that are needed to achieve convergence can be reduced by replacing classic genetic operators with different ones to guide the search through the solution space.

3. Alternatively, system-specific knowledge can be used to modify the genetic operators in such a way that they only result in viable solutions. This does not guide the search but prevents time loss due to the evaluation of many illegal solutions, which may arise from random variations in heavily restricted GA problems.

4. The population size needed to achieve convergence can be reduced by dynamically controlling candidate selection with a LS method.

5. System-specific knowledge can be used to construct a model to quickly approximate the results of fitness functions that are expensive to calculate, speeding up the evaluation of the GA objectives.

It is worth noting that the possible resulting HGAs form a broad class of algorithms and that individual HGAs might fall under categories different from GA within the taxonomy of EA (Calegari et al., 1999).

3 Case study

3.1 Problem-specific variators

Within the field of water network design optimization, algorithms that guide the GA to reduce the size of the search space is a specific challenge in current research (Maier et al., 2014). Table 1 lists a collection of genetic operators that was composed to tune a GA to the optimization of a least-cost design (Alperovitz and Shamir, 1977; Savic and Walters, 1997). This type of problem varies pipe diameters throughout the network in search of the minimum network costs while achieving a minimum pressure at each node. In addition to several classic GA variators (Holland, 1995; Goldberg, 1989), two heuristic variators are used that were constructed with the goal of a least-cost design in mind. In terms of the classification of hybrid metaheuristics by Talbi (2002), the resulting HGA is a low-level teamwork hybrid.

The heuristic flatiron mutator was custom-made to enhance convergence according to approach 2 in the list above. It guides the search past a type of artefact that commonly occurs in intermediate solutions for the least-cost design problem. This artefact occurs when classic mutation causes a larger diameter pipe to be surrounded by smaller diameter pipes, which is hydraulically insensible. These artefacts can take a long time to disappear through random mutation only. The flatiron mutator speeds up convergence by “smoothing out” these artefacts as follows:

1. For the mutating pipe, obtain the neighbour IDs from a lookup table with neighbouring pipes per pipe (it is worth noting that this lookup table is created at the start of the optimization, thereby limiting its impact on computation).

2. If the pipe connects to exactly 1 or 2 neighbouring pipes, compare the diameter of the mutating pipe to those of its neighbours.

3. If the mutating diameter is larger than the diameter of all neighbours, reduce it to the largest diameter among neighbours.

The heuristic list proximity mutator enhances convergence according to approach 3 in the list above. It is equivalent to the classic “creep mutator” (Sivanandam and Deepa, 2007): it functions as the regular random mutation of a single pipe diameter, except that the possible outcomes of the mutation are limited to values close to the value prior to mutation. This mutator is typically used because large deviations from the original diameter are likely to cause hydraulically inviable solutions.

In order to evaluate the influence of the developed problem-specific variators, a series of tests was performed on a case study.

3.2 Case study network

The case study consists in the design of part of the existing drinking water distribution network of the Dutch village Sittard. The network has a total length of 10.8 km and has 1000 connections, including connections to a school, a residential building with 32 apartments and a care farm for mental patients. The network is fed by a single reservoir and has a mean total demand of 15 m³ h⁻¹. The network is represented by an EPANET (Rossman, 2000) model consisting of 583 junctions, 491 pipes, 140 valves and 1 reservoir. The network is displayed in Fig. 1.

Figure 1 EPANET model of the drinking water distribution network of Sittard (Netherlands), consisting of 583 junctions, 491 pipes, 140 valves and 1 reservoir.

3.3 Optimization

For the design of the network, the minimization of the product between pipe diameter and pipe length (surrogate for costs) was considered as the objective, constrained by a minimum pressure at each node equal to 34 m. The decision variables were the pipe diameters that could be chosen from the following: 0, 13.2, 21.2, 36, 42.6, 58.2, 66, 72.8, 87.3, 101.6, 130.8, 147.6, 163.6, 190, or 200 mm. A population of 100 individuals with an elitism rate of 15 % was used for each optimization. Selection between candidates was achieved through tournament selection with a tournament size of 2 and with the objective function – the product of pipe length and diameter – as the performance criterion.

3.4 Tests

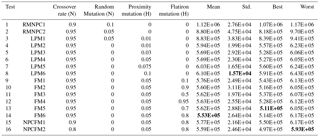
A total of 16 tests were performed, wherein different rates for the specific variators were considered in order to assess their influence on the network design results. For each test, a total of 1×10⁵ function evaluations and 10 runs were performed: each test was repeated 10 times in order to assess the mean, standard deviation, best and worst results obtained for each test. Table 2 provides an overview of the different tests, including the considered variator values and obtained results. Tests 1 and 2 consist of different rate combinations of the classical random mutation (RM) and one-point crossover (NPC). The heuristic proximity mutation was added in tests 3 to 8. Different rates for the heuristic flatiron mutation were considered in tests 9 to 14. Tests 15 and 16 further explore the influence of the one-point crossover on the performance of the algorithm.

Table 2 Problem-specific variator values considered in the different tests and obtained results for 10 runs with 1×10⁵ function evaluations each. The best results are indicated in bold.

4 Results

From the obtained results (Table 2) it is clear that the consideration of the heuristic flatiron mutation (FM) and proximity mutation (LPM) significantly improved the obtained results for the optimization problem. These results are graphically reported in Fig. 2.

Figure 2 Overview of the obtained results for the different tests.

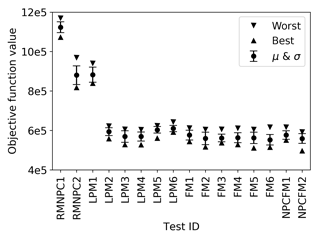
Considering only the naïve random mutation and one-point crossover, the best results after 1×10⁵ function evaluations were achieved with a mutation rate equal to 0.05 and a crossover rate equal to 0.95. In this case the average objective function value was 8.8×10⁵. Adding a proximity mutation does not improve the results, but considering only a proximity mutation and no random mutation has a significant influence on the outcomes. With only the proximity mutation, the best results after 1×10⁵ function evaluations were achieved for a proximity mutation rate of 0.05. With this value, the best results were achieved for the mean as well as the best and worst values for the objective function. Figure 3a illustrates the influence of this variator on the computed objective function values.

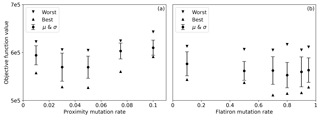
Figure 3 (a) Influence of the proximity mutation rate on the obtained objective function values in tests LPM2, LPM3, LPM4, LPM5 and LPM6. (b) Influence of the flatiron mutation rate on the obtained objective function values in tests FM1, FM2, FM3, FM4, FM5 and FM6.

Adding a flatiron mutation further improved the obtained results. The best results after 1×10⁵ function evaluations, on average, were obtained for a combination of a crossover rate of 0.95, with a proximity mutation rate equal to 0.05 and a flatiron mutation rate equal to 0.8. The best result within one test was obtained for a slightly lower flatiron mutation rate, equal to 0.7. Figure 3b illustrates the influence of this flatiron mutation rate on the obtained objective function values.

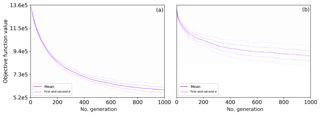
The effect of the problem-specific variators can also clearly be seen on the shape of the convergence curves. Figure 4 illustrates the mean, mean ± standard deviation, and mean ±2 × standard deviation convergence curves for tests number 2 (RMNPC2) and 12 (FM4). The proximity and flatiron mutations lead to smoother curves and a faster convergence. The standard deviation between results of the different runs is also much lower, which means that the results are more stable.

Figure 4 Convergence curves (mean, first and second standard deviations of 10 runs) obtained for tests RMNPC2 and FM4. (a) One-point crossover, proximity mutation and flatiron mutation (FM4). (b) Random mutation and one-point crossover (RMNPC2).

5 Discussion and conclusions

The results presented in this paper clearly illustrate the value of applying heuristic, non-classical variators in drinking water distribution system design optimizations using genetic algorithms. While the difference between the test with random mutation and the other tests is especially noticeable in Fig. 2, it is worth noting that the smaller differences between the other individual tests indicate a significant difference in convergence as well. In Fig. 4a, for instance, it can be seen that, in FM4, the average objective function value of 6×10⁵ was reached in around 700 generations, about 1.4 times faster than in LPM2, LPM5 and LMP6.

In the tests, the combination of a low rate for the proximity mutation with a high rate of the flatiron mutation leads to the best results after 1×10⁵ function evaluations (test numbers 13:FM5 and 14:FM6), i.e. the fastest convergence. All tested combinations which include either the flatiron or the proximity mutation exhibit a similar or worse performance. Albeit slower, particularly stable results were obtained with the proximity mutation (rate = 0.1) and no flatiron mutation. These runs show the smallest standard deviation in the results after 1×10⁵ function evaluations.

In future research and consulting projects with Gondwana, this combination of variators will be used in order to deal with the computational challenges of larger real-world networks.